
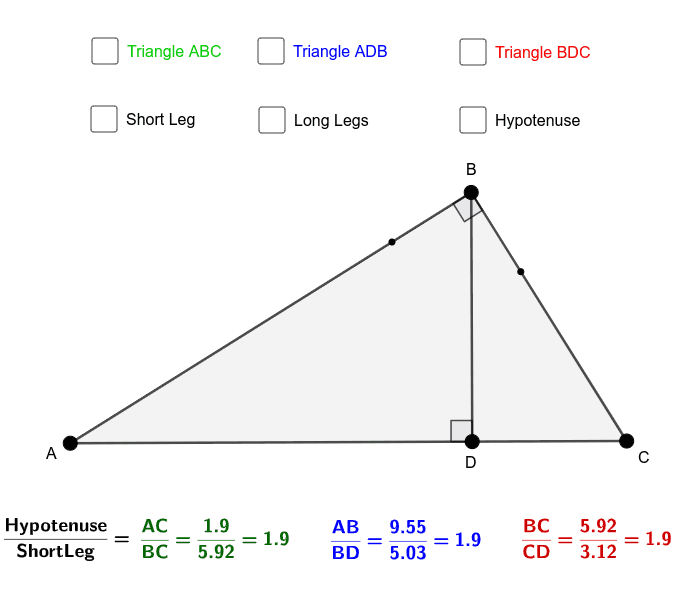
There is a special type of scenario that happens with similar right triangles. For more on similar triangles, check out this post here. This means they can be different in size (smaller or larger) but if they have the same angles and the sides are in proportion, they are similar! Triangles can be proven similar by AA, SAS, or SSS. When two triangles have equal angles and proportionate sides, they are similar. Similar Right Triangles (with Altitude drawn): In an acute triangle, all altitudes lie within the triangle.
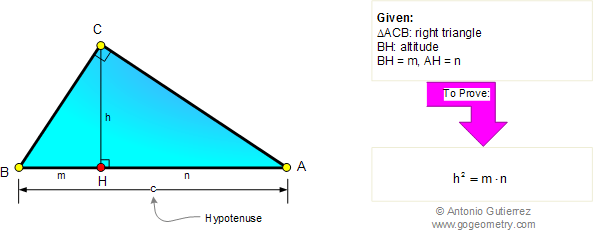
Whichever method you choose, do what makes most sense to you! Happy calculating! In each triangle, there are three triangle altitudes, one from each vertex. Although, I go over the long way to solve this problem, there is also short cut many people use called the “geometric means” which is also briefly mentioned in this post (under the Tip! section). where 'h' is the altitude of the right triangle and 'x' and 'y' are the bases of the two similar triangles formed after drawing the altitude from a vertex to the hypotenuse of the right triangle.
Altitude geometry right triange how to#
We are going to take this step by step on how to solve a problem like this. The formula to calculate the altitude of a right triangle is h xy. So it's okay to have an altitude that is not inside your triangle.Greetings math peeps and welcome to another week of MathSux! In todays post we are going to explore how to find the legs of a right triangle when an altitude is drawn from the vertex to its hypotenuse. If I look at the other two altitudes in this obtuse triangles, we're going to have one altitude going like that I'm going to have to extend that side as well and we'll drop down another altitude. Right Triangle Altitude Theorem Part a: The measure of the altitude drawn from the vertex of the right angle of a right triangle to its hypotenuse is the. Notice that I had to extend that opposite side. So if we pick this vertex, our opposite sides are over here but that opposite side doesn't continue to where this altitude will drop. So a third case is the obtuse triangle, and here is where I say to a line containing the opposite side.

However if I pick my 90 degree angle as my vertex, then we'll be able to see that altitude inside the triangle. If I pick this vertex right here the altitude will just be that leg of the triangle. That's going to be that leg of the triangle. If we look at a right triangle over here we can see that if I pick this vertex right here, we already have an altitude drawn. Notice that all three altitudes are inside the triangle. We would have two more altitudes, each of which would go perpendicular to the opposite side. So if I were to pick this top vertex right here, the altitude would go straight down perpendicular to the opposite side. So if we look at an acute triangle, there are going to be three altitudes, one form each vertex. It's not always to the opposite side and you're going to see why in a second here. For oblique, obtuse triangles: the altitude dropped from the obtuse angle will be inside the triangle and the other two altitudes will fall outside the triangle. So this definition is written very carefully. Right Triangle Similarity Theorem If the altitude. What we're talking about is a perpendicular segment, remember this symbol right here means perpendicular-I'm trying to get you used to seeing these symbols-from a vertex to a line containing the opposite side. Have students share the problems that they developed in Activity 4.5.4. When we're talking about triangles, there's a special segment three in each triangle called an "Altitude." So we're not talking about skiing here.


 0 kommentar(er)
0 kommentar(er)
